Zu Beginn der LETs wurde unser Bienenhaus geliefert. Das Material wog insgesamt mehr als 250kg. Wir trugen zuerst die Teile hoch, aber da es sehr rutschig war, sind wir auch oft ausgerutscht, was sich in einer recht durchgängigen Erdschicht auf unserer Kleidung manifestiert hat. Noch dazu war das Rad einer unserer beiden Scheibtruhen ohne Luft, sodass wir das Meiste ohne Transporthilfen zum Zielort schaffen mussten.
Sobald wir mit dem Transport fertig waren, sortierten wir das gesamte Material, in etwa in der Reihenfolge, wie wir es für die Bau benötigen würden.
Dann mussten wir den Boden begradigen, was sehr schiwerig war. Wie wir alle wissen, liegt unsere Schule ja auf einem Berg. Die Fläche auf der die Hütte gebaut werden sollte, war also nicht gerade. Wir mussten ein großes Rechteck in die Erde graben (ca. 20-40cm tief). Wir haben es geschafft, eine in etwa gerade Fläche hinzukriegen, ganz exakt gerade ist sie aber nicht geworden. Was aber nicht wirklich etwas ausgemacht hat, da wir geplant hatten, die Hütte sowieso auf einen Rahmen zu stellen, der auf Erdpflöcken montiert sein würde. Wir müssen also nur darauf achten, später die Erdpflöcke so in die Erde zu hämmern, dass von Erdpflock zu Erdpflock eine gerade horizontale Linie entsteht.
Den Rahmen zu machen, der als Basis der gesamten Hütte dienen sollte, war auch eher schwierig, da der Rahmen unbedingt im Rechten Winkel sein musste. Kontrolliert haben wir das, indem wir beide Diagonalen gemessen hatten. Wenn sie gleich lang sind, ist der Rahmen im rechten Winkel.
Wir haben also zwei Maßbänder genommen und die beiden Diagonalen gleichzeitig gemessen. Den Rahmen haben wir dann so verändert, bis beide Strecken gleich lang waren.
Damit wir nicht aus der Übung kommen, mussten wir zwei Rahmen bauen: Einer war im Bausatz enthalten, den anderen haben wir selber dazu- und eingebaut. Dieser zweite, nicht im Lieferumfang enthaltene Rahmen, sollte dazu dienen die Höhe der Hütte im Innenraum zu vergrößern (damit große Menschen sich nicht den Kopf stoßen).
Wir haben uns entschlossen, keine Beton-Piloten zu verwenden, sondern (wie schon weiter oben erwähnt) Erdspieße, auf die wir den Rahmen aufschrauben wollen. Dafür haben wir acht 80cm lange Erdspieße gekauft die wir in den Boden einschlagen wollten. Zunächst haben wir mit einem Erdspieß versucht, ob das überhaupt funktioniert (der Boden auf unserem Grundstück ist sehr steinig). Nachdem sich der erste Erdspieß ganz gut einschlagen ließ, haben wir dann begonnen auch die anderen sieben Spieße einzuschlagen.
Bei der Nivellierung des Rahmens mussten wir darauf achten, dass alle Erdspieße auf der selben Höhe waren. Deswegen mussten wir manchmal den bereits eingeschlagenen Erdspieß wieder herausziehen und anderswo einschlagen. Außerdem hat uns der Umstand, dass sich beim Einschlagen der Spieße die Schraubplatte verdreht hat, großes Kopfzerbrechen bereitet, da dann plötzlich die Schraublöcher nicht mehr unter dem Rahmen zu liegen kamen.
Im Bausatz enthalten, war der erste Rahmen den wir mit viel Mühe zusammengeschraubt, mit unserer Diagonalen-Messmethode in den Rechten Winkel gebracht und auf die Erdspieße aufgelegt haben. Das Ausnivellieren des Rahmens mit der Wasserwaage war allerdings sehr schwierig. Mehrfach mussten wir Erdspieße wieder aus der Erde zeihen und neu einschlagen, bis alle vier Seiten des Rahmens „in der Waage“ waren.
Nachdem das geschafft war, haben wir die Fundamenthölzer am Rahmen angeschraubt. Den zweiten Rahmen für den wir das Material extra gekauft hatten, mussten wir noch zuschneiden und auf die Fundamenthölzer aufschrauben.
Nachdem auch der zweite Rahmen endlich im Rechten Winkel eingerichtet, am ersten Rahmen montiert und nivelliert war, konnten wir mit dem Bau der Wände und der Verlegung des Fußbodens beginnen.
Gerade der Aufbau der Wände war oft sehr mühsam da die Bretter sehr verzogen waren und deswegen nicht gepasst haben. Das Befestigen der Fußbodenbretter mit Nägeln war eine gute Übung für uns, Nägel gerade in ein Werkstück zu bringen. Wir haben bei dieser Arbeit gesehen wie einfach das Nägel-Einschlagen ist, wenn man ein paar Regeln beherzigt. Die interessanteste war, dass man den Hammer eher Locker un weiter hinten am Stiel hat und ohne Kraftaufwand aus dem Handgelenk von oben auf den Nagel fallen lässt. Durch das Gewicht des Hammers wird impulsförmig Druck auf den Nagel ausgeübt, der ihn ins Holz treibt.
Trotz all dieser Schwierigkeiten, sind wir während der Leitstudie fast bis zur Dachkonstruktion gekommen und können nun die Hütte in der 6. Leitstudie fertig bauen und streichen.
Kategorie: Leitstudien 2017/18
Planung des Bienenhaus
Wir arbeiten gerade an einem Plan für das Bienenhaus. Wir haben mittlerweile eine Skizze des Grundrisses und werden innerhalb der nächsten Leitstudien-Stunden die Planung vollenden und versuchen dannach die wichtigsten Punkte vom Plan auf das Gelände in die Wirklichkeit zu übertragen. Danach werden wir entscheiden ob wir Erde abtragen müssen. Entschprechend muss auch der Plan angepasst werden (siehe weiter unten).
Plan unseres Bienengarten Hauses
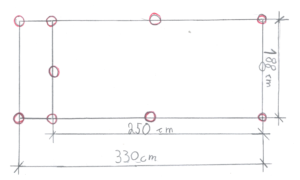
10 Betonpfeiler für den Boden
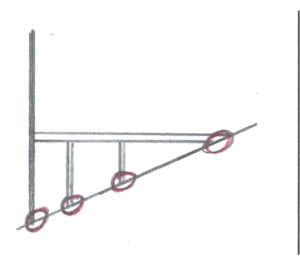
Hebelgesetz
Das Hebelgesetz
Am Beispiel einer Waage ist das Hebelgesetz leicht zu verstehen. Die Waage bleibt im Gleichgewicht, wenn das Produkt aus Kraft mal Abstand vom Drehpunkt auf beiden Seiten gleich ist. Daraus folgt das Hebelgesetz:
Kraft · Kraftarm = Last · Lastarm
F1 · r1= F2 · r2
Die Begriffe Kraftarm und Lastarm sind missverständlich, wenn man nicht mit Sicherheit sagen kann, welches nun die Last und welches die (die Last bewegende) Kraft ist. Wenn man sie stattdessen mit Hebel 1, Hebel 2 usw. bezeichnet, kommt man ebenso zum Ziel.
Masse, Gewichtskraft, Gewicht und über Newton
Masse
Die Masse ist eine absolute Größe und ist überall gleich.
Wenn ein Ball auf der Erde eine Masse von 2 kg hat, dann hat er überall diese Masse (die Masse wird in kg ausgedrückt).
Gewichtskraft
Die Gewichtskraft gibt an, wie schwer der Gegenstand scheint
(sie ist eine relative Größe).
Wenn der Ball auf der Erde 2kg wiegt, dann er zwar auf dem Mond auch eine Masse von 2kg, aber er scheint leichter wegen der geringeren Gewichtskraft.
Die Gewichtskraft rechnet mann durch die Formel F=m*a aus.
(F=Force (Kraft) m=Masse a=Fallgeschwindlichkeit).
Gewicht
Das Gewicht wird in kg angegeben. „Gewicht“ ist in der Physik aber kein klar definierter Begriff. In der Physik gibt nur die Masse und die Gewichtskraft (wie oben beschrieben).
Newton
Sir Isaac Newton war ein Englischer Physiker und entdekte, dass nicht nur die Erde eine Schwerkraft hat, sondern jeder Gegenstand, aber bei z.B. einem Apfel, kann man diese Kraft wegen der geringen Mass nicht spüren.
Alles was sich Newton dazu überlegt hat, verpackte er in einem Merksatz
| Merksatz: Die Schwerkraft zwischen 2 Körpern ist anziehend und umso größer,je größer die Masse der Körpern ist. Die Schwerkraft nimmt mit Abstandder Körper zueinander ab: Bei dem doppeltem Abstand ist die Kraft nurmehr ein Viertel so groß. |
Kräfte
Kräfte:
Zunächst einmal etwas Simples: Bewegende Objekte wollen immer in Bewegung bleiben und ruhende Objekte wollen immer ruhend bleiben.
Newton:
So! Habt ihr schon mal was von Newton gehört? Auf jeden Fall, hier ist die Erklärung:
1 Newton ist jene Kraft, die man benötigt, um 1kg Masse 1 sek. lang zu bewegen, so dass sie 1 m/s zurück legt.
Angriffspunkt:
Lasst uns ein Experiment zu dem Angriffspunkt zusammen machen! 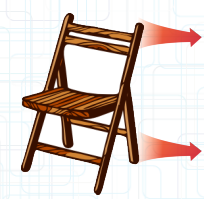 Nehmt euch einen Stuhl. Wenn ihr jetzt an dem oberen Ende des Stuhles anzieht, kippt er! Wenn ihr unten anzieht rutscht er in die Richtung in die ihr zieht. Man sieht, dass der Angriffspunkt der Kraft ausschlaggebend dafür ist, wie sich der Gegenstand, auf den die Kraft einwirkt, bewegt.
Nehmt euch einen Stuhl. Wenn ihr jetzt an dem oberen Ende des Stuhles anzieht, kippt er! Wenn ihr unten anzieht rutscht er in die Richtung in die ihr zieht. Man sieht, dass der Angriffspunkt der Kraft ausschlaggebend dafür ist, wie sich der Gegenstand, auf den die Kraft einwirkt, bewegt.
Gegenkraft:
Wir haben es fast geschafft! Es fehlt nur noch die Gegenkraft. Also jedes Objekt hat eine Gegenkraft! Wenn ihr auf einen Tisch drückt drückt er gegen euch. Somit bleib eure Hand auf der Tischplatte.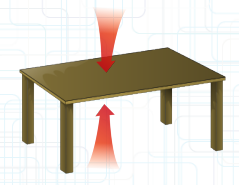
Über Rollen und Flaschenzüge
Der Flaschenzug –
lose und feste Rollen
Der Flaschenzug
… ist ein System womit man schwerere Dinge leichter hochheben bzw. hochziehen kann.
Man kann den Kraftaufwand zum Hochziehen reduzieren, indem man Rollen zum Flaschenzug hinzufügt. Allerdings: je mehr Rollen man hat, desto mehr Seil muss gezogen werden.
Das heißt :
4 Rollen =jeder Strang trägt 25% des Gewichts – man muss also nur mit 25% der Gewichtskraft am Seil anziehen, braucht aber den 4-fachen Weg (d.h. man muss viermal soviel Seil ziehen, als bei einer einfachen festen Rolle).
6 Rollen= jeder Strang trägt 16,6% des Gewichts. D.h. nur 16,6% des Gewichtes, aber 6 mal soviel Seil.
Eine feste Rolle ist so befestigt, dass sie ihre Position während der Benutzung nicht ändert. Mittels fester Rollen werden Kräfte umgelenkt. Es muss also eine gleich große Kraft aufgewendet werden. Wir haben bei einer festen Rolle also keine Kraftersparnis. Manchmal ist es jedoch einfacher eine Kraft in eine andere Richtung aufzubringen. Die folgende Grafik zeigt eine feste Rolle sowie die mathematischen Zusammenhänge.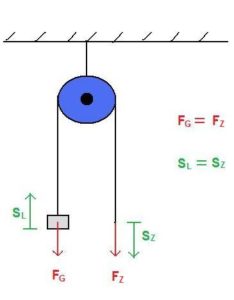
Lose Rollen:
Lose Rollen liegen in der Seilführung und werden vo
m Seil getragen. Jeder der beiden Teile des Seils, die die lose Rolle einschließen, nimmt 50% der Kraft auf. Auf diese Weise lässt sich eine Last mit dem halben Kraftaufwand heben. Allerdings ist der Zugweg dabei doppelt so lang.
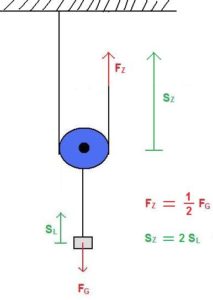
Auch hier gilt also wieder das „Goldene Gesetz der Mechanik“:
Was man an Kraft spart, muss man an Weg zusetzen.
Dieses Gesetz gilt für alle kraftumformenden Einrichtungen. Sie wurde vor ca. 400 Jahren von dem italienischen Naturwissenschaftler GALILEO GALILEI (1564-1642) formuliert.
Die Reibung
Die Reibung
Wenn man einen Ball einmal anstöst würde er – in einem idealen, reibungsfreien System – für immer weiterrollen. Aber da es in einem realen System immer Reibung gibt, bleibt der Ball nach einiger Zeit liegen.
Reibung entsteht, wenn sich zwei Körper berühren. Dadurch, dass die Oberflächen von Körpern oft glatt aussehen, aber in Wirklichkeit nie glatt ist, kommt es zur Reibung.
Es gibt drei Arten von Reibung.
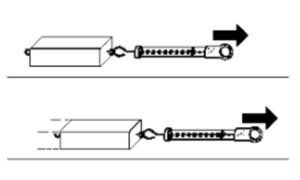
Bevor sich der Holzkotz (im Bild oben) in Bewegung setzt, ist der Ausschlag des Newtonmeters (der Federwaage) am größten. Diesen Effekt nennt man dann Haftreibung.
Wenn der Klotz in Bewegung ist, nimmt die Reibungskraft ab. Hier spricht man von Gleitreibung.
Am geringsten ist die Reibung, wenn man Rollen unter den Klotz legt. Diesen Fall nennt man Rollreibung.
Reibung kann auch sehr nützlich sein, z.B. beim Autofahren wegen der Bodenhaftung der Reifen (besonders wichtig beim Bremsen), beim Radfahren – mit Hilfe der Gleitreibung zwischen den Bremsbacken und der Felge kann kann man bremsen usw.
Formeln:
Gewichtskraft
Fg= m*g
Gewichtskraft ist gleich Masse mal Anziehungskraft (auf der Erde ist das die Erdbeschleunigung = 9,81 m/s²
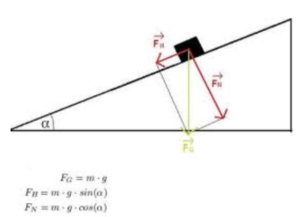
Kräfteparallelogramm:
Portraitfotografie
Für ein gutes Portrait muss man folgendes beachten:
man braucht einen Fotografen, eine Person die man fotografiert und natürlich eine Kamera.
Auf dieser sollte man paar Dinge wie folgt einstellen:
Am Modusrad sollte „A“ oder „Av“( je nach Hersteller der Kamera) gewählt werden. Diese Einstellung bewirkt, dass die Kamera automatisch die richtige Belichtungszeit einstellt, abhängig davon, welche Blende vom Fotografen gewählt wurde. Bei der Portraitfotoagrafie stellt man eine möglichst große Blendenöffnung (das bedeutet eine kleine Blendenzahl) ein. Scharf gestellt wird auf die Augen des Models. Außerdem achtet man darauf, dass das Gesicht gut aus geleuchtet ist.
von Lia, Stella, Sophie und Alva
Geometrische Optik
Geometrische Optik
Beispiel eines Strahlengangs im Kepler-Fernrohr, der den Ort des Zwischenbildes bei FOB, FOK zeigt.
Die geometrische Optik oder Strahlenoptik bedient sich des Strahlenmodells des Lichtes und behandelt damit auf einfache, rein geometrische Weise den Weg des Lichtes auf Linien.
Einem auf eine Linie begrenzten Lichtstrahl kommt keine physikalische Realität zu, und man kann ihn folglich auch nicht experimentell realisieren. Dennoch lässt sich mit Hilfe der Strahlenoptik die Funktion der optischen Abbildung, die die Hauptaufgabe der technischen Optik ist, oft mit ausreichender Genauigkeit beschreiben.
Beschränkt man die geometrische Optik auf Strahlen, die die optische Achse sehr flach schneiden, liegt die sogenannte paraxiale Optik vor. Dafür lassen sich geschlossene mathematische Ausdrücke für Abbildungsgleichungen finden. Man wendet diese Methode aber hauptsächlich nur dann an, wenn man sich einen schnellen grundsätzlichen Überblick verschaffen will, bevor man umfangreiche Ermittlungen genauer durchführt.
Die geometrische Optik lässt sich mathematisch als Grenzfall der Wellenoptik für verschwindend kleine Wellenlängedes Lichts auffassen. Sie versagt aber auch in diesem Fall, wenn die Verhältnisse für Strahlen mit hoher Energiedichte oder nahe an der Grenze zum Schatten (kein Licht) untersucht werden sollen.
Axiome der geometrischen Optik
Als allgemeinste Grundlage der Strahlenoptik lässt sich das Fermatsche Prinzip ansehen. Es führt auf die beiden ersten der folgenden Axiome.
- Axiom: In homogenem Material sind die Lichtstrahlen gerade.
- Axiom: An der Grenze zwischen zwei homogenen isotropen Materialien wird das Licht im Allgemeinen nach dem Reflexionsgesetz reflektiert und nach dem Brechungsgesetzgebrochen.
- Axiom: Der Strahlengang ist umkehrbar, die Lichtrichtung auf einem Lichtstrahl ist belanglos.
- Axiom: Die Lichtstrahlen durchkreuzen einander, ohne sich gegenseitig zu beeinflussen.
Anwendungen
Hauptanwendungsgebiet der Strahlenoptik ist die Behandlung der Abbildung durch optische Elemente, Geräte und Systeme, wie Linsen, Brillen, Objektive, Fernrohre und Mikroskope.
Auch das Raytracing-Verfahren in der 3D-Computergrafik beruht auf den Gesetzen der geometrischen Optik.
Die Luftspiegelungen durch eine heiße Luftschicht über sonnenbeschienenem Asphalt und andere Naturphänomene können auch durch Anwendung dieses Prinzips erklärt werden.
Grenzen
Effekte, die von der geometrischen Optik nicht beschrieben werden können, sind unter anderem:
die Beugung, die das Auflösungsvermögen optischer Instrumente begrenzt. Sie kann nur im Rahmen der Wellenlehre oder der Quantenmechanik verstanden werden.
die Interferenz, die ebenfalls durch die Wellenlehre oder Quantenmechanik erfassbar ist, und die z. B. für die Wirkungsweise der Antireflexbeschichtung von wesentlicher Bedeutung ist.
die Polarisation, die quantenmechanisch mit dem Spin der Photonen zu tun hat, aber auch mit der Wellenlehre erklärbar ist. Sie ist im Zusammenhang mit der Doppelbrechung von Bedeutung, und auch für die teilweise Reflexion an brechenden Flächen, wo sie die Quantität des reflektierten Lichts beeinflusst.
Wir haben sehr viel spass mit diese Projegt gehabt